99

Technical Research |Abstracting the Human Systems

98

Technical Research |Abstracting the Human Systems

add() — add vectors

sub() — subtract vectors

mult() — scale the vector with multiplication

div() — scale the vector with division

mag() — calculate the magnitude of a vector

setMag() - set the magnitude of a vector

normalize() — normalize the vector to a unit length of 1

limit() — limit the magnitude of a vector

heading() — the 2D heading of a vector expressed as an angle

rotate() — rotate a 2D vector by an angle

lerp() — linear interpolate to another vector

dist() — the Euclidean distance between two vectors (considered as points)

angleBetween() — find the angle between two vectors

dot() — the dot product of two vectors

cross() — the cross product of two vectors (only relevant in three dimensions)

random2D() - make a random 2D vector

random3D() - make a random 3D vector

A list of Vector operations that can be used within Processing.

These operations can be defined by simple words within processing, but It is important to understand how these operations work to understand how to utilize them within the simulation.

From Shiffman, “Chapter 1. Vectors.”

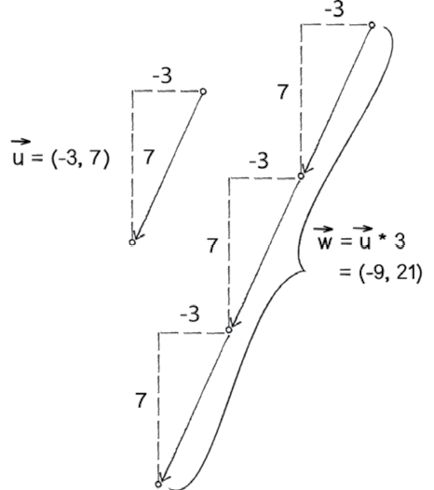
Vector Multiplication

It can be seen from this figure that multiplying a vector keeps its direction, but increases its length. As such, vector multiplication can be used as a way to scale the magnitude of vectors.

From Shiffman, “Chapter 1. Vectors.”

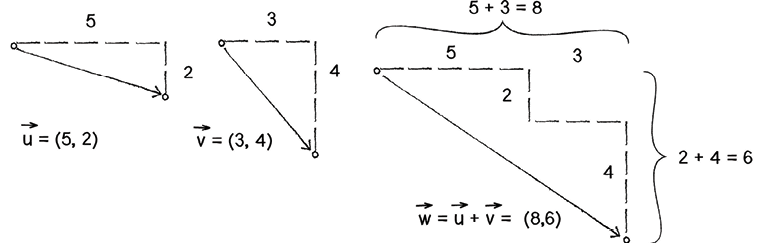
Vector Addition

adding two vectors together results in a new vector location that is the result of going along each vector individually. As such this can be utilized to update position by adding additional vector forces to it.

From Shiffman, “Chapter 1. Vectors.”

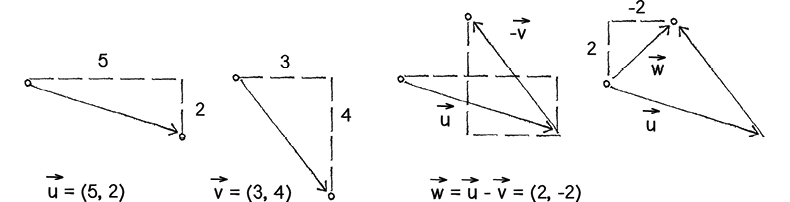
Vector Subtraction

Vector subtraction can be used to calculate the distance between two points, which in turn have many uses within a crowd simulation, such as determining how far away an object is to the agent or calculating a vector that points from the agent to its goal.

From Shiffman, “Chapter 1. Vectors.”

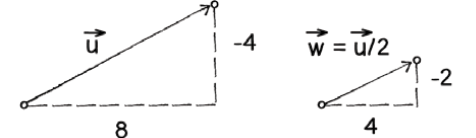
Vector Division

Dividing a vector by a scalar value is similar to multiplying it, except its length is decreased instead of increased. Dividing a vector by itself will normalize a vector and result in a magnitude of 1. This normalized vector can then be scaled by multiplying the vector by a scaler variable in order to control how big a vector can become.

From Shiffman, “Chapter 1. Vectors.”