97

Technical Research |Abstracting the Human Systems

96

Technical Research |Abstracting the Human Systems

Pathfinding

The Pathfinding system determines how these agents move within the simulation. If they decide to go to a door, how do they walk over? If there are other people in the way, how do they avoid them? If there are walls, how do they not bump into them? While this system is the most technical and dynamic of the three—as it deals with real-time calculations due to environmental inputs—it is also the most well-established, as it can be described relatively intuitively by Craig Reynolds’ description of the three layers of motion: action selection, steering, and locomotion. These steps, much like the human systems defined earlier in this chapter, are hierarchal and feed into the next.

Locomotion

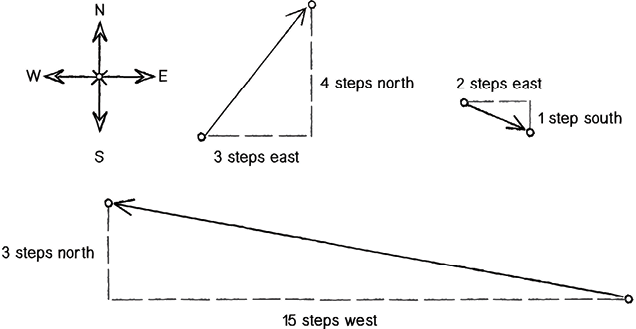
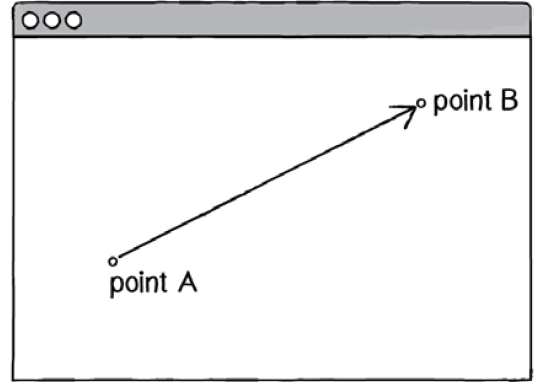
The bottom level contains Locomotion, which is the method by which the vehicles move to their goals. There are many ways to calculate this in machine logic, but relating back to the physical world, its kinematics can be broken down into position, velocity, and acceleration.[2] In programming, these can be expressed by vectors, which can be defined as entities that have both magnitude and direction.[3] These vectors can be thought of as the difference between two points, and can be used to describe the location and movement of autonomous agents within the virtual space.[4] (Fig. 2.3.4 - 6) This virtual space, much like the physical world, can be understood in the three spatial dimensions of x, y, and z. As such, these vectors can be broken down in the same way to describe the agent’s relation within virtual space. By familiarizing oneself with these vectors, and their relations within these spatial dimensions, one can begin to calculate and manipulate these vectors to establish a variety of possible functions.[5] (Fig. 2.3.7 - 11)

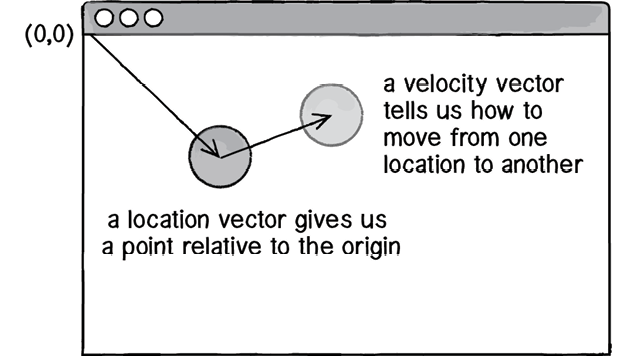
From this model, it is then possible to describe position with a vector that determines a point relative to the origin, whereas velocity can be described with a vector that determines a point relative to position (the rate of change of position), and acceleration can be described with a vector that determines a point relative to velocity (the rate of change of velocity). To utilize these vectors in this way, one can add them into one another to calculate the resulting position of the agent. In simpler terms, the software will take the following steps every frame to achieve motion:

Calculate Acceleration

Add Acceleration to Velocity

Add Velocity to Position

Draw object at Position.

When the software runs, it is essentially re-rendering an object at the point of its location every time the frame is refreshed. This means a velocity of 0 would entail no change in location from the previous frame, and an acceleration of 0 would mean constant velocity. (Fig. 2.3.12) This trickledown effect produces non-linearity within vehicle movements, producing greater complexity within the system.

Vectors can be thought of as the difference between 2 points.

From Daniel Shiffman, “Chapter 1. Vectors,” in The Nature of Code (United States: D. Shiffman, 2012), accessed October 17, 2019, https://natureofcode.com/book/chapter-1-vectors/.

Vectors can be described by 2 scaler variables.

From Shiffman, “Chapter 1. Vectors.”

Velocity vector updates position

This figure shows how adding a velocity vector to position vector calculates a new position vector for the agent to move to.

From Shiffman, “Chapter 1. Vectors.”