103

Technical Research |Abstracting the Human Systems

102

Technical Research |Abstracting the Human Systems

Steering

The next level up is steering, which is the calculated force that is applied to the vehicle to tell it how it should move. The key word here is force, which in traditional Newtonian motion can be defined as a vector that causes an object with mass to accelerate.[15] Looking back at the steps in locomotion, it can be seen that step one requires a vector that represents acceleration to determine to location of the agent, therefore in this stage, it is imperative to find a way to calculate that acceleration.

Shiffman relates this concept back to the physical world by investigating Newton’s second law of motion—which states that Force = mass x acceleration ()—and then solving for acceleration, producing the formula: acceleration = Force / Mass. From this, Shiffman remarks, “Now, in the world of Processing, what is mass anyway? Aren’t we dealing with pixels? To start in a simpler place, let’s say that in our pretend pixel world, all of our objects have a mass equal to 1. F/ 1 = F. And so: A = F.”[16] This makes sense in the context of a crowd simulation, as the calculated force is a translation of behavior, and not a relation to the object’s mass—such as gravity. What this means is that to calculate the acceleration vector in locomotion, one must first calculate a steering force that can be added to the acceleration vector.

This steering force can be an accumulation of many forces within the system and can represent many things, ranging from wind to friction to gravity, etc. depending on the simulation. While these forces can seem complex, Craig Reynolds developed a simple formula to calculate the steering force within these models:[17] (Fig. 2.3.13 - 14)

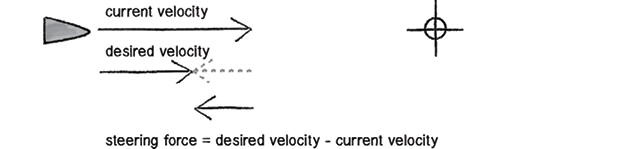
Steering Force = Desired Velocity – Current Velocity

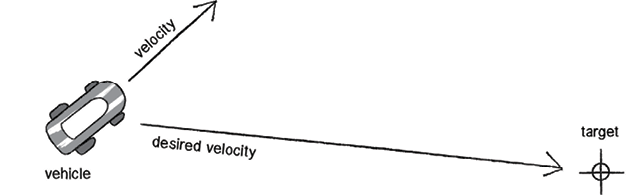
This formula then requires two variables: the desired velocity and the current velocity. The current velocity can already be derived from the last frame of locomotion; therefore, the critical part of this calculation is determining the desired velocity. This is a vector that points from the agent’s current position to the target position, therefore it can be calculated by the formula:[18] (Fig. 2.3.15)

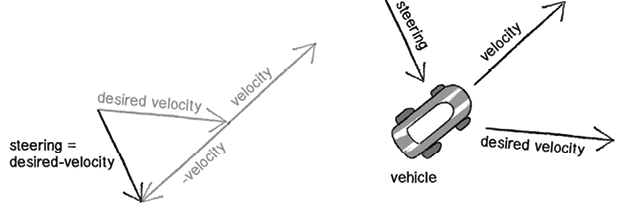
Desired velocity = Target Position – Agent Position

Vectors as stated earlier are entities that have both magnitude and direction. With these two equations in place, the direction of the steering force can be calculated. One thing to keep in mind, however, is the magnitude of such forces. Much like how humans do not instantly get from one location to the next, they also do not instantly turn from one direction to another. As such, this stage will require

The calculated opposing Steering force, when added to current velocity, will bring it closer to desired velocity

From Daniel Shiffman, “Chapter 6. Autonomous Agents,” in The Nature of Code (United States: D. Shiffman, 2012), accessed October 17, 2019, https://natureofcode.com/book/chapter-6-autonomous-agents/.

The steering force is pushing down on the vehicle to steer it towards desired velocity

From Shiffman, “Chapter 6. Autonomous Agents.”

Desired velocity can be calculated by obtaining the Vector distance between the vehicle position and agent position

From Shiffman, “Chapter 6. Autonomous Agents.”

We must then limit this distance vector to obtain our desired velocity so our vehical, or human, can’t move too fast

From Shiffman, “Chapter 6. Autonomous Agents.”

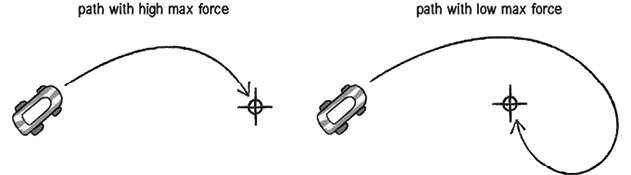
How Max force can affect radius

From Shiffman, “Chapter 6. Autonomous Agents.”